VF state value

State value of Value Function

Objective function

• $v(s)$: true state value
• $\hat{v}(s,w)$: estimated state value
• goal: find an optimal $w$ so that $\hat{v}(s,w)$ can best approximate $v(s)$ for every $s$
• policy evaluation problem, later we will extend to policy improvement

To find the optimal $w$, we need two steps:

1. define an objective function
2. derive algorithms for optimizing the objective function

The objective function

$$J(w)=\mathbb{E}[(v(S)-\hat{v}(S,w){)}^2]$$

• goal: find the best $w$ that can minimize $J(w)$
• the expectation is with respect to the random variable $S\in \mathcal{S}$

如何求上面这个期望呢？

上面这个期望其实也可以写成${\mathbb{E}}_S$，如果想求出来期望就必须先知道random varible S的分布；我们之前是怎么求期望的呢？之前都是可以通过Monte Carlo大量模拟的方法去求得期望的，但这里用模拟的方法求期望变得不太现实，退而求其次，我们可以用模拟的方法求得S的分布，得到分布求期望就可以写成概率形式的平均了。

What is the probability distribution of $S$?

• This is new. In the tabular method, we do not need to consider this.
• There are several ways to define the probability distribution of $S$.
  • uniform distribution: $P(S=s)=\frac{1}{|\mathcal{S}|}$
  • stationary distribution: $P(S=s)=d_{\pi }(s)$, where $\pi$ is a given policy

Uniform distribution

• treat all the states to be equally important
• the objective function becomes $$J(w)=E[(v(S)-\hat{v}(S,w){)}^2]=\frac{1}{|\mathcal{S}|}\sum _{s\in \mathcal{S}}(v_{\pi }(s)-\hat{v}(s,w){)}^2$$
• drawback: the states may not be equally important
  • some states may be rarely visited by a policy
  • does not consider the real dynamics of the Markov process under the given policy

Stationary distribution

• describes the long-run behavior(长期行为) of a Markov process
• Stationary distribution(稳态分布)
• let $\{d_{\pi }(s){\}}_{s\in \mathcal{S}}$ denote the stationary distribution of the Markov process under policy $\pi$
• the objective function becomes weighted squared error $$J(w)=E[(v(S)-\hat{v}(S,w){)}^2]=\sum _{s\in \mathcal{S}}{d}_{\pi }(s)(v_{\pi }(s)-\hat{v}(s,w){)}^2$$
• more frequently visited states have higher values of $d_{\pi }(s)$
  • their weights in the objective function are also higher than those rarely visited states
• More detail, see stationary distribution

Optimization algorithms

• use gradient-descent algorithm to minimize the objective function $J(w)$ $$w_{k+1}=w_k-{\alpha }_k{\nabla }_{w}J(w_k)$$
• the true gradient is $$\begin{array}{rl}{\nabla }_{w}J(w)& ={\nabla }_w\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w){)}^2]\\ & =\mathbb{E}[{\nabla }_w(v_{\pi }(S)-\hat{v}(S,w){)}^2]\\ & =2\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w))(-{\nabla }_w\hat{v}(S,w))]\\ & =-2\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w)){\nabla }_w\hat{v}(S,w)]\end{array}$$ the true gradient involves the calculation of an expectation

Then we have

$$\begin{array}{rl}{w}_{k+1}& =w_k-{\alpha }_k{\nabla }_{w}J(w_k)\\ & =w_k+2{\alpha }_k\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w_k)){\nabla }_w\hat{v}(S,w_k)]\end{array}$$

Use stochastic gradient to replace the true gradient($2{\alpha }_k$ merges to ${\alpha }_k$)

$$w_{k+1}=w_k+{\alpha }_k(v_{\pi }(s_t)-\hat{v}(s_t,w_k)){\nabla }_w\hat{v}(s_t,w_k)$$

• we don’t know the true state value $v_{\pi }$ here, solution:
  • use the methods in TD, replace $v_{\pi }$ by another value(approximation)
  • use MC, replaced by $g_t$
  • use TD, replaced by $r_{t+1}+\gamma \hat{v}(s_{t+1},w_k)$

Implementation

$$\boxed{\begin{array}{rl}& \text{Algorithm}\text{TD Learning of State Values with Function Approximation}\\ & \text{Initialization: }\text{Differentiable function }v(s,w)\text{ with initial parameter }{w}_0.\\ & \text{Goal: }\text{Learn the true state values of a given policy }\pi .\\ & \text{For each episode }\{(s_t,r_{t+1},s_{t+1}){\}}_t\text{ generated by }\pi ,\text{ do:}\\ & \text{For each sample }(s_t,r_{t+1},s_{t+1}),\text{ do:}\\ & \text{General case:}\\ & w_{t+1}\leftarrow w_t+{\alpha }_t\left[r_{t+1}+v(s_{t+1},w_t)-v(s_t,w_t)\right]{\nabla }_{w}v(s_t,w_t)\\ & \text{Linear case (with features }\varphi (s)\text{):}\\ & w_{t+1}\leftarrow w_t+{\alpha }_t\left(r_{t+1}+\varphi (s_{t+1}{)}^{\top }{w}_t-\varphi (s_t{)}^{\top }{w}_t\right)\varphi (s_t)\end{array}}$$

这里仅仅是做了estimate the state values of a given policy (policy evaluation)

Selection of function approximators

How to select the function $\hat{v}(s,w)$?

• use a linear function approximator
  • $\hat{v}(s,w)={\varphi }^{\top }(s)w$ ($\hat{v}(s,w)=w^{\top }\varphi (s)$)
  • $\varphi (s)$: feature vector(polynomial basis, fourier basis) of state $s$
  • widely used before
• use a neural network as a nonlinear function approximator
  • input: state $s$
  • output: estimated state value $\hat{v}(s,w)$
  • parameters: weights and biases of the neural network

Linear function approximator

Linear function approximator: $\hat{v}(s,w)={\varphi }^{\top }(s)w$, then we have

$${\nabla }_w\hat{v}(s,w)=\varphi (s)$$

Substituting the gradient into the above TD algorithm

$$w_{t+1}=w_t+{\alpha }_t\left[r_{t+1}+\gamma v(s_{t+1},w_t)-v(s_t,w_t)\right]\varphi (s_t)$$

yields

$$w_{t+1}=w_t+{\alpha }_t\left[r_{t+1}+\gamma {\varphi }^{\top }(s_{t+1})w_t-{\varphi }^{\top }(s_t)w_t\right]\varphi (s_t)$$

which is the algorithm of TD learning with linear function approximation(TD-Linear)

优缺点

• 缺点：难以选择合适的特征向量(feature function $\varphi$不好选)
• 优点：理论性质更好，线性函数逼近的理论性质比非线性函数逼近更好(可解释可理解)
  • tabular representation是linear fuction representation的特例

Tabular representation(special case)

Show that tabular representation is a special case of linear function representation

• Consider a special feature vector for state $s$: (one-hot encoding) $$\varphi (s)=e_s\in {\mathbb{R}}^{|\mathcal{S}|}$$ where $e_s$ is a vector with the $s$-th entry as 1 and the others as 0
• In this case: $$\hat{v}(s,w)={\varphi }^{\top }(s)w=e_s^{\top }w=w(s)$$ where $w(s)$ is the $s$-th entry of $w$
• Recall that the TD-Linear algorithm is $$w_{t+1}=w_t+{\alpha }_t\left(r_{t+1}+{\varphi }^{\top }(s_{t+1})w_t-{\varphi }^{\top }(s_t)w_t\right)\varphi (s_t)$$ When $\varphi (s)=e_s$, the above algorithm becomes $$w_{t+1}=w_t+{\alpha }_t\left(r_{t+1}+w_t(s_{t+1})-w_t(s_t)\right)e_s$$ This is a vector equation that merely updates the $s_t$-th entry of $w_t$
• Multiplying $e_s$ on both sides of the equation gives $$w_{t+1}(s_t)=w_t(s_t)+{\alpha }_t\left(r_{t+1}+w_t(s_{t+1})-w_t(s_t)\right)$$ which is exactly the tabular TD algorithm (which is called TD-Table here)

Summary: TD-Linear becomes TD-Table if we select a special feature vector(one-hot encoding)

Illustrative examples

Consider a 5x5 grid-world example:

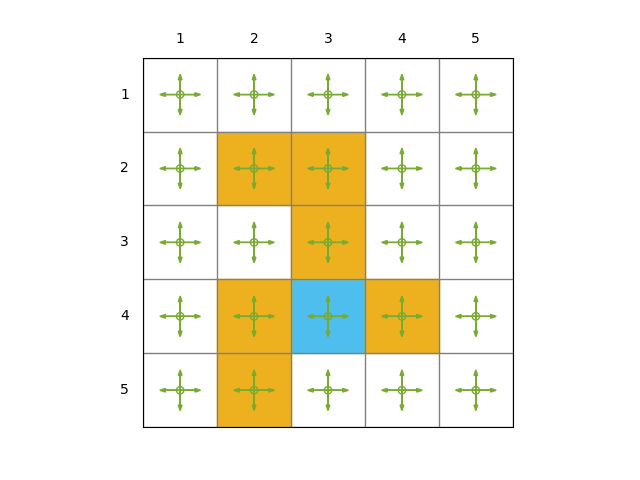
• Given a policy $\pi (a|s)=0.2$ for any $s\in \mathcal{S},a\in \mathcal{A}$
• The rewards are $r_{\text{forbidden}}=r_{\text{boundary}}=-1$, $r_{\text{target}}=1$, and $\gamma =0.9$
• The goal is to estimate the state values of this policy
  • There are 25 state values in total
  • TD-Table: 25 parameters
  • TD-Linear: less than 25 parameters

通过之前的policy evaluation的方法，我们可以得到ground truth的state values

True State Values 2D	True State Values 3D

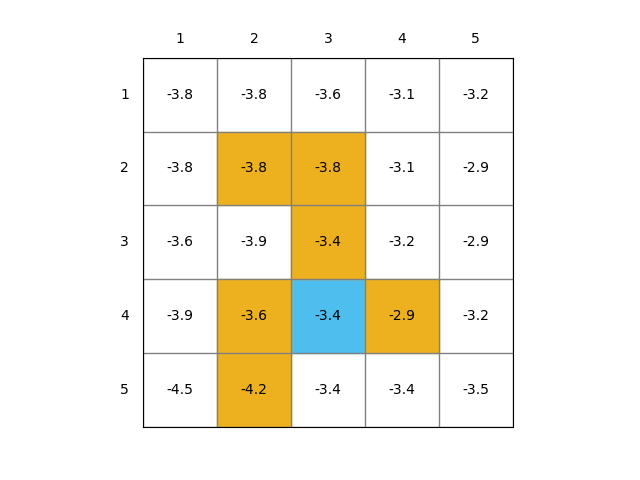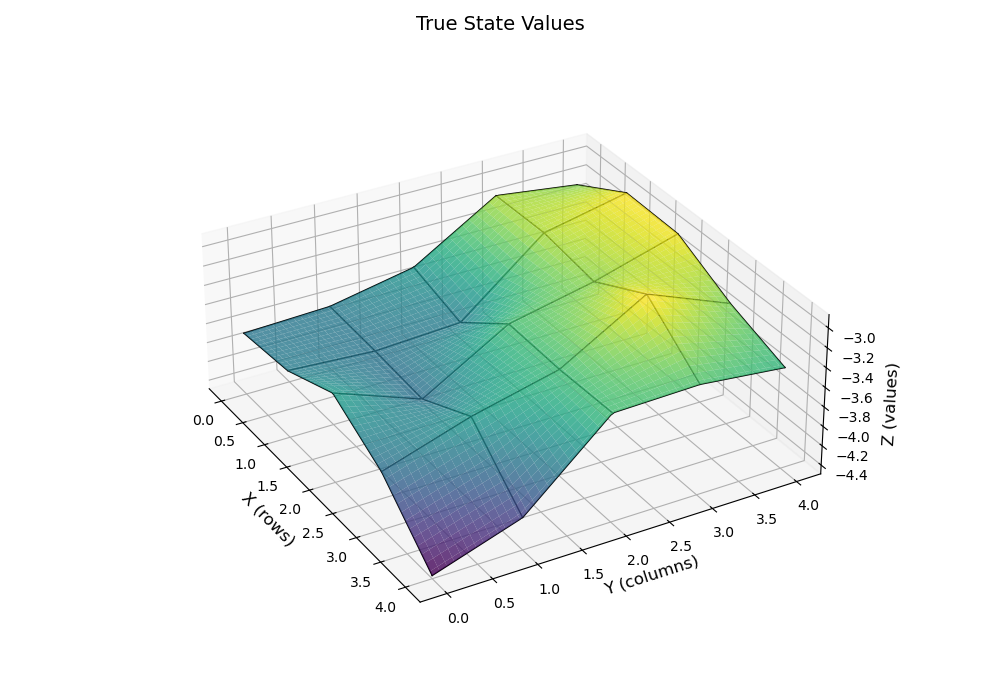下面我们分别使用TD-Table和TD-Linear来估计这些state values，其中

• 500 episodes were generated following the uniform policy $\pi$
• each episode has 500 steps and starts from a randomly selected state-action pair(following a uniform distribution)
• TD-Table: ${\alpha }_t=0.005$
• TD-Linear: ${\alpha }_t=0.0005$, $\varphi (s)=(1,x,y)$

自己实现的结果如下：

TD-Table	TD-Linear($\varphi (s)\in {\mathbb{R}}^3$)

RMSE结果对比：

More Details

• the code above is open-source at donglinkang2021/grid_world
• more about the basis function result, see
  • polynomial basis
  • fourier basis
• more about how to visualize a matrix see visualize_matrix

Summary of the story

• objective function: $$J(w)=\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w){)}^2]$$
• gradient-descent algorithm: $$w_{t+1}=w_t+{\alpha }_t\left[v_{\pi }(s_t)-v(s_t,w_t)\right]{\nabla }_w\hat{v}(s_t,w_t)$$
• the true value function $v_{\pi }$ is replaced by an approximation $\hat{v}$: $$w_{t+1}=w_t+{\alpha }_t\left[r_{t+1}+\gamma \hat{v}(s_{t+1},w_t)-\hat{v}(s_t,w_t)\right]{\nabla }_w\hat{v}(s_t,w_t)$$

Theoretical analysis (optional)

The algorithm

$$w_{t+1}=w_t+{\alpha }_t\left[r_{t+1}+\gamma \hat{v}(s_{t+1},w_t)-\hat{v}(s_t,w_t)\right]{\nabla }_w\hat{v}(s_t,w_t)$$

does not minimize the following objective function:

$$J(w)=\mathbb{E}[(v_{\pi }(S)-v(S,w){)}^2]$$

• Objective function 1: True value error $$J_E(w)=\mathbb{E}[(v_{\pi }(S)-v(S,w){)}^2]=\Vert \hat{v}(w)-v_{\pi }{\Vert }_D^2$$ where $\Vert x{\Vert }_D=x^{\top }Dx$ and $D$ is a diagonal matrix(each element is the stationary distribution $d_{\pi }(s)$ of the corresponding state)
• Objective function 2: Bellman error $$J_{BE}(w)=\Vert \hat{v}(w)-\underset{\text{replace }{v}_{\pi }}{\underbrace{(r_{\pi }+\gamma P_{\pi }\hat{v}(w))}}{\Vert }_D^2=\Vert \hat{v}(w)-T_{\pi }(\hat{v}(w)){\Vert }_D^2$$ where $T_{\pi }(x)\doteq r_{\pi }+\gamma P_{\pi }x$
• Objective function 3: Projected Bellman error $$J_{PBE}(w)=\mathbb{E}[(\hat{v}(w)-M{T}_{\pi }(\hat{v}(w)){)}^2]=\Vert \hat{v}(w)-M{T}_{\pi }(\hat{v}(w)){\Vert }_D^2$$ where $M$ is a projection matrix
• The TD-Linear algorithm minimizes the projected Bellman error