Visualize Matrix
Introduction
这一节作为附录中的一节是有原因的,其原因就在于当时自己在复现赵老师的VF state value的代码时遇到一个问题:如何可视化一个2D的matrix?这个问题看似很简单,但自己在一开始时还真卡住了,自己最开始的可视化效果是类似这样的:
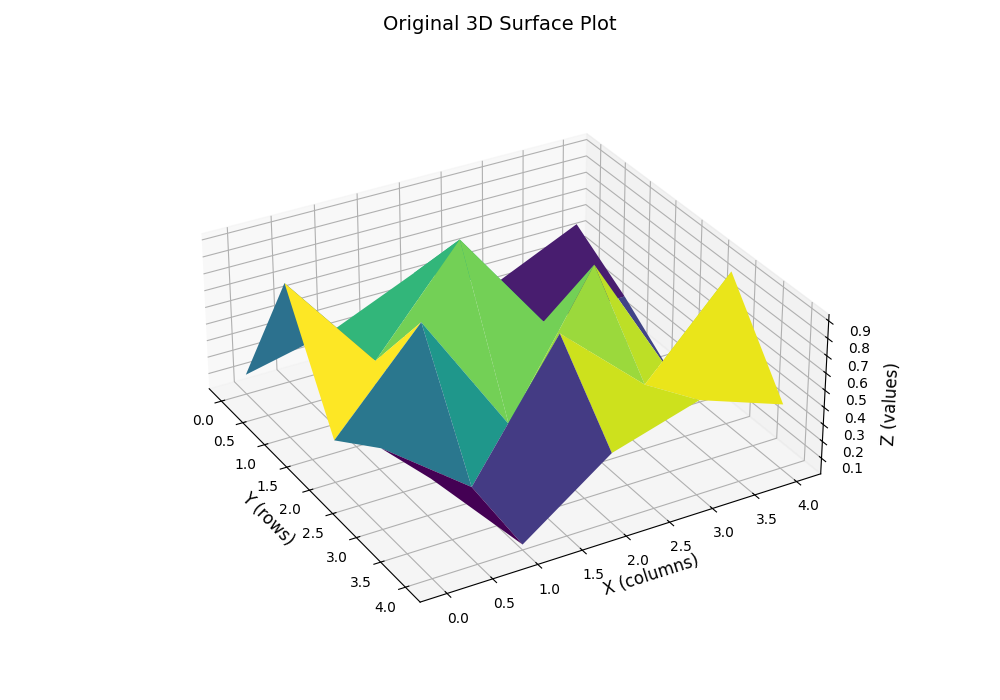
但是这样的效果非常的丑陋,仅仅是由不同的state value的顶点组成的几个平面,并没有很直观的展示出state value的大小关系。所以自己就去问了下deepseek,最终找到了一个比较好的方法,就是使用scipy的RectBivariateSpline来进行线性插值(k=1),然后再进行可视化。这样的效果就会好很多,如下图所示:
小插曲
DeepSeek一开始给自己的代码是设置了
k=3的,给自己生成了曲面的效果,但自己希望的是保留上面原始的平面效果,只是在平面上进行插值,然后自己觉得这种方法是不对的,于是就又分别找了chatgpt和Claude等等模型问了,最后给的答案都没有deepseek好:要么是给自己生成三角化的平面,要么是使用错误的函数,最后自己重新决定看文档,最终发现了RectBivariateSpline这个函数原来是可以线性插值的(k=1)。当一个东西不work的时候,要非常清楚为什么其不work再找下一个方法,这样起码一直再做减法,不用回溯。
另外得区分一下本章的插值和VF state value的区别,之前的任务的目的是为了估计state value,得到state value附近的值只是一个顺带的效果,而本章的目的是为了可视化一个2D的matrix,就是假设已经得到state value的值了,目的是如何在其周围插值更好。
运用本节的方法,可以可视化之前的结果得到如下的效果:
| Smoothed (k=1) | Smoothed (k=2) | Smoothed (k=3) |
|---|---|---|
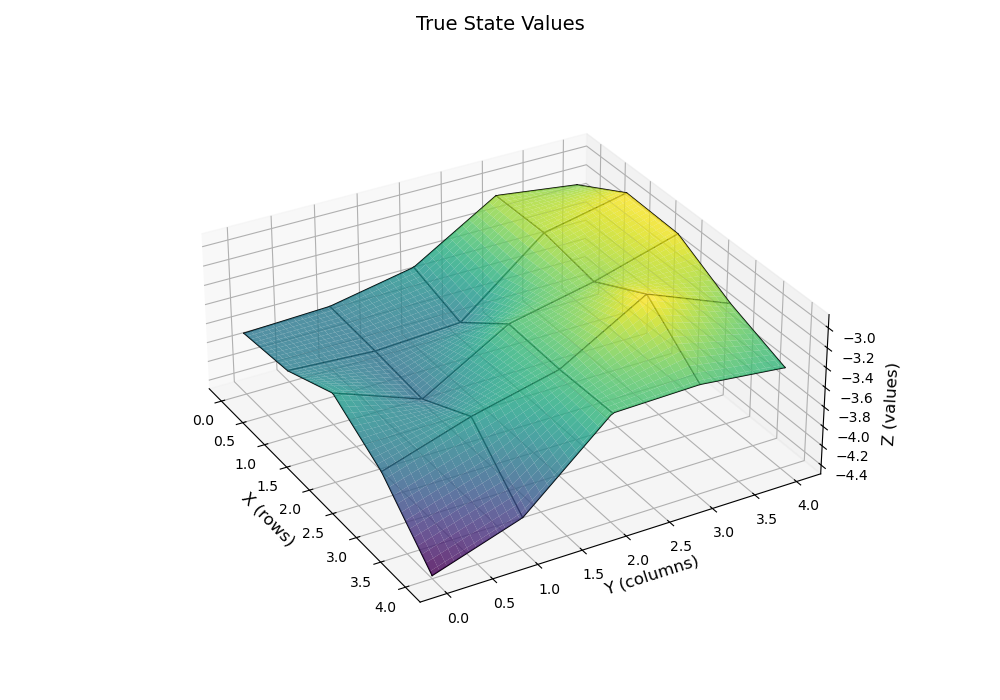 | .png) | .png) |
Results
本章仅仅做展示几个效果,具体的代码可以参考Appendix。
| Original | Smoothed (k=1) | Smoothed (k=2) | Smoothed (k=3) |
|---|---|---|---|
 | .png) | .png) | .png) |
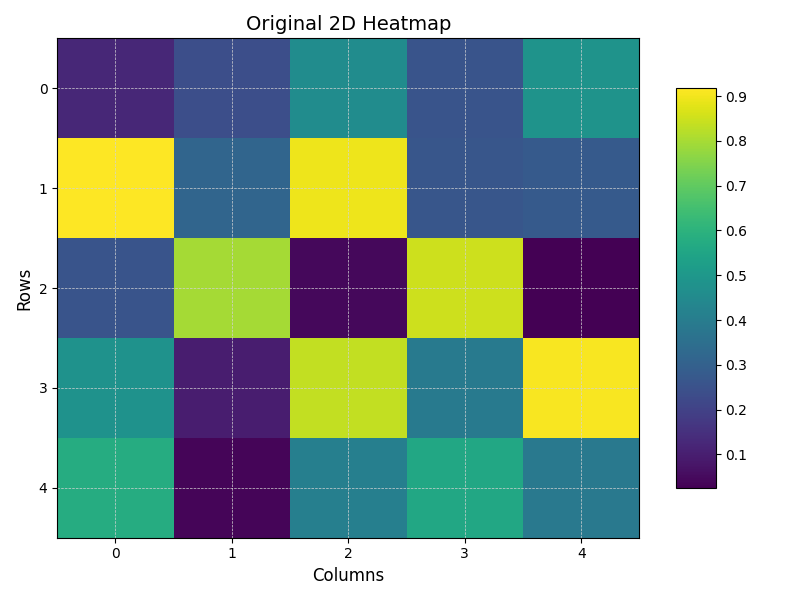 | .png) | .png) | .png) |
Appendix
复现本节Results中的八张图的代码如下:
python show_matrix.py# File: show_matrix.py
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import RectBivariateSpline
from pathlib import Path
Path("results").mkdir(exist_ok=True)
def grid_matrix2d(matrix2d:np.ndarray):
"""
Generate grid coordinates for 2D matrix visualization
Args:
matrix2d (np.ndarray): Input 2D numerical matrix
Returns:
X (np.ndarray): Column coordinate grid matrix with same shape as input matrix
Y (np.ndarray): Row coordinate grid matrix with same shape as input matrix
Z (np.ndarray): Original matrix values with unchanged shape
Notes:
- Uses *ij-indexing* to generate grid, maintains row/column orientation consistent with original matrix
- X corresponds to column indices, Y corresponds to row indices (opposite of conventional Cartesian system)
- Returned grid coordinates can be directly used for matplotlib 3D surface plotting
"""
m, n = matrix2d.shape
y = np.arange(m)
x = np.arange(n)
Y, X = np.meshgrid(y, x, indexing='ij')
return X, Y, matrix2d
def smooth_grid_matrix2d(matrix2d:np.ndarray, k:int, n_points:int):
"""
Perform bilinear interpolation smoothing on a 2D matrix
Args:
matrix2d (np.ndarray): Input 2D numerical matrix
k (int): Interpolation order, default=1 (bilinear interpolation), increase for higher-order interpolation
n_points (int): Number of interpolation points per dimension
Returns:
X_new (np.ndarray): Interpolated column coordinate grid matrix (2D array)
Y_new (np.ndarray): Interpolated row coordinate grid matrix (2D array)
Z_new (np.ndarray): Interpolated value matrix (2D array)
Notes:
- Uses SciPy's `RectBivariateSpline` for bivariate spline interpolation
- Maintains ij-indexing coordinate system where X corresponds to column direction, Y to row direction (opposite of conventional Cartesian system)
- `grid=True` parameter ensures return of 2D grid format data, directly usable for 3D surface plotting
- Interpolated grid points are evenly distributed within original matrix coordinate range
- Example: When n_points=100, generates a 100x100 smooth grid
"""
m, n = matrix2d.shape # Get number of rows and columns
# Generate original row and column coordinates (x for columns, y for rows)
y_orig = np.arange(m)
x_orig = np.arange(n)
# Create bilinear interpolation function
interp_func = RectBivariateSpline(y_orig, x_orig, matrix2d, kx=k, ky=k)
# Generate dense interpolation points (using n_points points in this example)
y_new = np.linspace(0, m-1, n_points)
x_new = np.linspace(0, n-1, n_points)
# Calculate interpolated Z values
Z_new = interp_func(y_new, x_new, grid=True)
# Generate grid point coordinates
Y_new, X_new = np.meshgrid(y_new, x_new, indexing='ij')
return X_new, Y_new, Z_new
def draw_matrix2d(matrix2d:np.ndarray, title:str):
X, Y, Z = grid_matrix2d(matrix2d)
# Draw 3D surface plot
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(Y, X, Z, cmap='viridis', edgecolor='none')
# Set aspect ratio
ax.view_init(elev=30, azim=330)
ax.set_box_aspect([2.5, 2.5, 1])
# Set axis labels
ax.set_ylabel('X (columns)', fontsize=12)
ax.set_xlabel('Y (rows)', fontsize=12)
ax.set_zlabel('Z (values)', fontsize=12)
ax.set_title(title, fontsize=14)
# Add color bar
# fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)
plt.tight_layout()
plt.savefig(f"results/{title.replace(' ','_')}.png")
def draw_matrix2d_smooth(matrix2d:np.ndarray, title:str, k:int, n_points:int=100):
X, Y, Z = smooth_grid_matrix2d(matrix2d, k, n_points)
# Draw 3D surface plot
fig = plt.figure(title, figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(
Y, X, Z,
cmap='viridis',
alpha=0.8,
edgecolor='none'
)
# Add gridlines on the interpolated surface
m, n = matrix2d.shape
# Draw gridlines along x direction
for i in range(n):
# Find the corresponding index in the dense grid
idx_x = int(i / (n-1) * (n_points-1))
# Extract the corresponding slice from Z
ax.plot(Y[:, idx_x], X[:, idx_x], Z[:, idx_x],
color='black', linestyle='-', linewidth=1)
# Draw gridlines along y direction
for j in range(m):
# Find the corresponding index in the dense grid
idx_y = int(j / (m-1) * (n_points-1))
# Extract the corresponding slice from Z
ax.plot(Y[idx_y, :], X[idx_y, :], Z[idx_y, :],
color='black', linestyle='-', linewidth=1)
# Set aspect ratio
ax.view_init(elev=30, azim=330)
ax.set_box_aspect([2.5, 2.5, 1])
# Set axis labels
ax.set_ylabel('X (columns)', fontsize=12)
ax.set_xlabel('Y (rows)', fontsize=12)
ax.set_zlabel('Z (values)', fontsize=12)
ax.set_title(title, fontsize=14)
# Add color bar
# fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)
plt.tight_layout()
plt.savefig(f"results/{title.replace(' ','_')}.png")
def draw_heatmap(matrix2d: np.ndarray, title: str, cmap: str = 'viridis'):
"""Draw a heatmap of a 2D matrix"""
fig = plt.figure(title, figsize=(8, 6))
ax = fig.add_subplot(111)
# Use imshow to draw heatmap
im = ax.imshow(matrix2d,
cmap=cmap,
aspect='auto',
origin='upper',
interpolation='nearest')
# Add color bar
fig.colorbar(im, ax=ax, shrink=0.8, aspect=10)
# Set axis labels
ax.set_xlabel('Columns', fontsize=12)
ax.set_ylabel('Rows', fontsize=12)
ax.set_title(title, fontsize=14)
# Add grid lines
ax.grid(visible=True,
color='lightgray',
linestyle='--',
linewidth=0.5)
# Set tick positions and labels
# 设置刻度间隔(每5个点显示一个标签)
step = max(1, matrix2d.shape[1] // 20) # 自动计算间隔,至少显示5个标签
xticks = np.arange(0, matrix2d.shape[1], step)
ax.set_xticks(xticks)
ax.set_xticklabels(xticks.astype(int)) # 转换为整数标签
# 对y轴做相同处理
step_y = max(1, matrix2d.shape[0] // 20)
yticks = np.arange(0, matrix2d.shape[0], step_y)
ax.set_yticks(yticks)
ax.set_yticklabels(yticks.astype(int))
plt.tight_layout()
plt.savefig(f"results/{title.replace(' ','_')}.png")
def _test_draw_matrix():
# Create a 5x5 matrix (example)
Z = np.random.rand(5, 5)
# Draw the 3D surface plot
draw_matrix2d(Z, 'Original 3D Surface Plot')
draw_matrix2d_smooth(Z, 'Smoothed 3D Surface Plot (k=1)', k=1)
draw_matrix2d_smooth(Z, 'Smoothed 3D Surface Plot (k=2)', k=2)
draw_matrix2d_smooth(Z, 'Smoothed 3D Surface Plot (k=3)', k=3)
draw_heatmap(Z, 'Original 2D Heatmap')
draw_heatmap(smooth_grid_matrix2d(Z,1,100)[2], 'Original 2D Heatmap (k=1)')
draw_heatmap(smooth_grid_matrix2d(Z,2,100)[2], 'Original 2D Heatmap (k=2)')
draw_heatmap(smooth_grid_matrix2d(Z,3,100)[2], 'Original 2D Heatmap (k=3)')
# plt.show()
if __name__ == '__main__':
_test_draw_matrix()